-
개념
- Neural Network에서 Mini Batch 단위로 입력되는 각 Layer의 입력을 정규화하여 학습을 안정화 시키는 학습 기술
Batch Normalization Layer에서 Normalization
- 기본 전제
- 전체 (N, 28, 28, 1) 데이터에 대해 batch_size = n 일 경우,
- Mini Batch = N/n개이고,
- 최초 Conv2D Layer의 kernel unit = 75, kernel size = (3, 3), input shape = (28, 28, 1)일 때
- 작동 원리
- 75개의 각 커널은 random하게 선택된 1개의 Mini Batch 내 모든 data point에 대해 Convolution 연산을 수행하고,
- 그 결과 값으로 각 data point에 대한 평균값과 분산값을 가지며,
- 1 Mini Batch 내 각 data point에 대한 평균값과 분산값을 활용하여 Data Point의 Normalize 가능
- 모든 Mini Batch가 학습되면서 Scale과 Shift 값이 학습
- BN Layer에서는 각 Mini Batch에서의 Scale과 Shift 값을 활용하여 해당 Mini Batch 내 데이터를 정규 분포 형태로 Normalize (재구성)
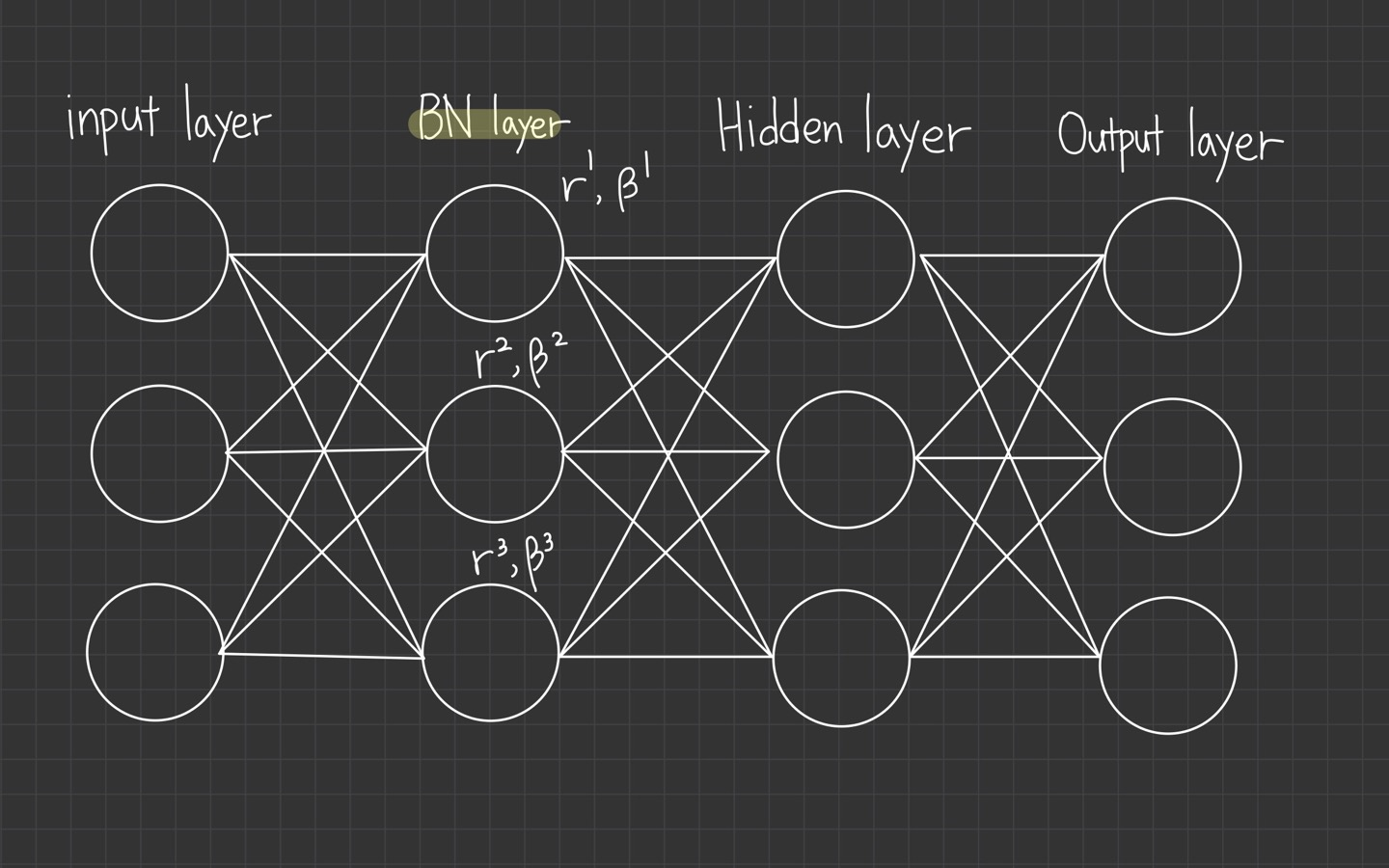
Batch Normalization Layer의 Parameter
- Trainable Parameter : Scale and Shift (Kernel 당 각 1개씩 존재)
- Non-Trainable Parameter : (Exponential) Mean Moving Average, Standard Average Deviation (평균의 평균 / 분산의 평균)
- Test 단계에서 최종적으로 학습 및 조정된 Scale, Shift, 평균의 평균, 분산의 평균이 전달
- Batch Normalization을 하는 이유
- Covariate Shift에 따른 Gradient Vanishing 문제 극복
- Train 단계에서,
- 무작위의 data points가 1개의 Mini Batch로 묶여 처리되는 과정에서, 1개의 Mini Batch 내 데이터 분포 차이가 발생할 수 있고,
- Neural Network의 Layer를 거치면서 내적에 따른 분포 변화, 및 Activation Function에 의한 비발화 데이터들의 소실로 인한 데이터 분포 차이가 가중화되어, Internal Covariate Shift가 발생할 가능성이 발생
- Internal Covariate Shift가 발생할 경우 Layer가 깊어질수록 Activation Function의 극값에 데이터가 밀집 분포할 우려가 발생하며,
- 그 결과 Gradient가 점진적으로 0으로 수렴하여 loss function의 최적화가 어려워지는 문제 발생
- Batch Normalization을 통해 극값에 밀집한 데이터를 정규분포화 하여 Gradient Vanishing 문제 극복 가능
- Validate과 Test 단계에서,
- Train data와 Validate 데이터 및 Test 데이터의 분포가 다를 경우 Overfitting 문제 발생 가능
- Batch Normalization을 통해 data Test 과정에서의 Overfitting 문제 예방 가능
